Ji-Cai Liu: A supercongruence related to Ramanujan-type formula for 1/π, 483-492

Abstract:

We prove a Ramanujan-type supercongruence involving the Almkvist-Zudilin numbers, which confirms a conjecture of Z.-H. Sun and is corresponding to Ramanujan-type formula for 1/π due to Chan and Verrill:

$$\sum_{k=0}^{\infty}\frac{4k+1}{(-27)^k}\gamma_k=\frac{3\sqrt{3}}{\pi}.$$

Here $\gamma_k$ are the Almkvist-Zudilin numbers.

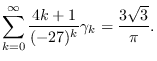Key Words: Supercongruences, Almkvist-Zudilin numbers, harmonic numbers.

2020 Mathematics Subject Classification: Primary 11A07; Secondary 05A19.

Download the paper in pdf format here.