Hajar Roshan-Shekalgourabi, Dawood Hassanzadeh-Lelekaami: On the equivalent properties of certain general local cohomology modules, 493-503

Abstract:

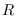
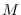
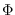
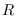
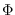
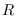
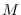
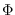
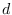
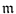
Let $R$ be a commutative Noetherian ring and $M$ be a ZD-module. In this paper, we investigate the Artinianness of general local cohomology modulus with respect to a system of ideals $\Phi$ of $R$. 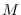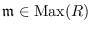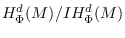For this aim, we introduce the concept of $\Phi$-Laskerian $R$-modules and we show that if $M$ is a $\Phi$-Laskerian module of finite dimension $d$ such that ${\frak m}$-relative Goldie dimension of any quotient of $M$ is finite for all ${\frak m} \in {\rm Max}(R)$, then $H^d_\Phi (M)/IH^d_\Phi (M)$ is Artinian for all $I\in \Phi$. 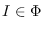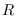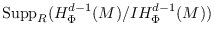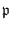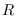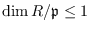Furthermore, if $R$ is semi-local, then ${\rm Supp}_R(H^{d-1}_\Phi (M)/IH^{d-1}_\Phi (M))$ is a finite set consisting of prime ideals ${\frak p}$ of $R$ with $\dim R/{\frak p} \leq 1$ for all $I\in \Phi$. 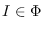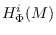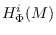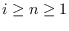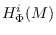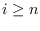Also, among other things, we provide a relationship between the vanishing and the finiteness of modules $H^i_\Phi (M)$ and we show that if $H^i_\Phi (M)$ is minimax for all $i \geq n \geq1$, then $H^i_\Phi (M)$ is Artinian for all $i \geq n$.

Key Words: Local cohomology modules, system of ideals, weakly Laskerian modules, ZD-modules, Artinian modules.

2020 Mathematics Subject Classification: Primary 13D45; Secondary 13E05, 13C05.

Download the paper in pdf format here.