In some previous papers , our attention focused on the
general theory of holomorphic subspaces in a complex Finsler space. In the
present paper two approaches in the study of complex curves of a complex
Finsler space will be proposed.
In the first section we study curves on the holomorphic tangent bundle
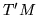
depending on the arc length parameter
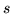
. This study is in
some sense through analogy with that made for curves in real Finsler spaces
by which an orthonormal moving frame of Frenet type is
introduced.
In the second part of the paper we study the geometry of a complex curve
(Riemannian surface) viewed as a particular one dimensional holomorphic
subspace. The induced tangent and normal Chern-Finsler connections and the
Gauss-Weingarden formulas will be obtained. A special attention is devoted
to its geodesic curvature.