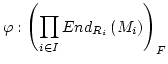
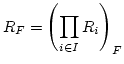 and
and
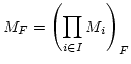 (theorem 1.1). Generally,
(theorem 1.1). Generally,
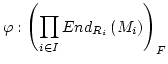
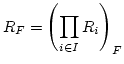 and
and
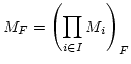 (theorem 1.1). Generally,
(theorem 1.1). Generally,
Key Words: Ultraproducts, rings of linear transformations, m-transitive rings, closed primitive rings.
2000 Mathematics Subject Classification: Primary: 03C20,
Secondary: 03C60, 16S50, 15A04, 16D60.
Download the paper in pdf format here.