Crina Boboc and S. Dascalescu :Good gradings of matrix algebras by finite abelian groups of prime index, p.5-11

Abstract:

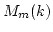
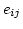
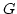
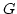
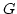
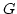
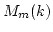
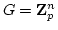
A group grading on a matrix algebra $M_m(k)$ is called good if all the matrix units $e_{ij}$ are homogeneous elements. 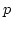We present a new way to classify good $G$-gradings by the orbits of a certain action of the group $G$ on a set of $G$-tuples of non-negative integers, and we use it to count the isomorphism types of good $G$-gradings on $M_m(k)$ in the case where $G={\bf Z}_p^n$ is a cyclic group of prime index $p$.

Key Words: Matrix algebra, group graded algebra, good grading.

2000 Mathematics Subject Classification: Primary: 16W50.

Download the paper in pdf format here.