Dorin Popescu and Marius Vladoiu:Strong Lefschetz property on algebras of embedding dimension three, p.75-86

Abstract:

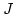
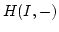
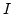
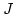
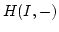
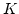
We show that "half" of the non-zero components of the generic ideal $J$ of a complete intersection ideal $I=(f_1,f_2,f_3)\subset K[x_1,x_2,x_3]$, with respect to the reverse lexicographic order, are uniquely determined by the Hilbert function $H(I,-)$ of $I$. Moreover the whole $J$ is uniquely given by $H(I,-)$ if and only if complete intersection standard graded $K$-algebras of embedding dimension 3 have strong Lefschetz property. Also we give some sufficient conditions for a semi-regular sequence to remain semi-regular after a permutation.

Key Words: Complete intersection, Fröberg conjecture, Lefschetz properties, semi-regular sequences.

2000 Mathematics Subject Classification: Primary: 13D40,
Secondary: 13P10, 13C40, 13D07.

Download the paper in pdf format here.