Marian Aprodu, Laura Filimon: Sections of $K3$ surfaces with Picard number two and Mercat's conjecture, 149-158

Abstract:

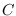
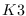
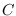
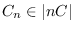
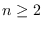
In [6, Theorem 1.1], the authors present counterexamples to Mercat's conjecture by restricting to a hyperplane section $C$ some suitable rank-two vector bundles on a $K3$ surface whose Picard group is generated by $C$ and another very ample divisor. We prove that the same bundles produce other counterexamples by restriction to hypersurface sections $C_n\in\vert nC\vert$ for all $n\ge 2$. 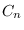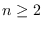In the process, we compute the Clifford indices of the corresponding hypersurface sections $C_n$, noting their non-generic nature for $n\ge 2$ (refer to Theorem 1). 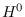A key ingredient to prove the (semi)stability of the restricted bundles, Theorem 2, is Green's Explicit $H^0$ Lemma (see [10, Corollary (4.e.4)]). 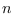In what concerns the (semi)stability, although general restriction theorems such as [9, Theorem 1.2] or [7, Theorem 1.1] are applicable for sufficiently large, explicit values of $n$, our approach works for all $n\ge 2$. 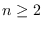It is also worth noting that our proof deviates slightly from the one presented in [6, Proposition 3.2]. 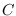Employing the same strategy leads to an enhancement of the main result of [21]; refer to Theorem 3 for counterexamples to the conjecture on curves in $\vert nC\vert$, where $C$ now acts as a generator of the Picard group.

Key Words: Higher-rank Brill-Noether theory, curves on $K3$ surfaces.

2020 Mathematics Subject Classification: Primary 14H60; Secondary 14H51, 14J60, 14J28.

Download the paper in pdf format here.