Let
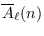
denote the number of
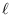
-regular
overpartitions of
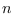
. Quite recently, Ray and Chakraborty
investigated the arithmetic density properties on powers of primes
satisfied by
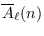
. Utilizing an algorithm of Radu
and Sellers, they proved a congruence modulo
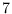
for
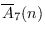
. Moreover, they stated without proof a
congruence modulo
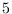
for
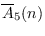
and a congruence
modulo
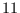
for
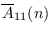
. For these three congruences,
they asked for an elementary proof. In this paper, we establish six
congruence families for these three partition functions, three of
which are the corresponding generalizations of three congruences
considered by Ray and Chakraborty.
-regular overpartitions, congruences, dissections, internal congruences.