Chuanan Wei, Chun Li: Two new $q$-congruences involving double basic hypergeometric series, 333-343

Abstract:

In this paper, we establish two new $q$-congruences involving double basic hypergeometric series. As conclusions, we give several congruences including the following one:

$$\sum_{k=0}^{p-1}\frac{(\frac{1}{2})_k^3(\frac{1}{4})_k}{(1)_k^44^k}\sum_{j=1}^{k}\bigg\{\frac{1}{(4j)^2}-\frac{1}{(2j-1)^2}\bigg\}$$

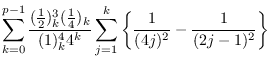$$\begin{align*}\quad\equiv \begin{cases}\displaystyle p\frac{(\frac{1}{2})_{(p-1)... ...$,}\\ [20pt] 0\pmod{p^2}, &\text{if $p\equiv 3\pmod 4$.} \end{cases}\end{align*}$$

where $p$ is an odd prime.

Key Words: $q$-Congruence, basic hypergeometric series, Watson's $_8\phi_7$ transformation formula, Gasper and Rahman's summation formula.

2020 Mathematics Subject Classification: Primary 11A07; Secondary 11B65.

Download the paper in pdf format here.