Julia Q. D. Du, Ziqian Wang, Liping Yuan: The total edge irregularity strength of hexagonal grid graphs, 157-177

Abstract:

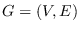
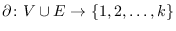
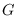
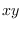
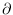
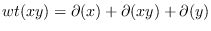
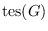
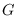
For a graph $G=(V,E)$, a labeling $\partial\colon V\cup E\rightarrow\{1,2,\ldots,k\}$ is called an edge irregular total $k$-labeling of $G$ if the weights of any two different edges are distinct, where the weight of the edge $xy$ under $\partial$ is defined to be $wt(xy)=\partial(x)+\partial(xy)+\partial(y)$. 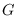The total edge irregularity strength $\mathrm{tes}(G)$ of $G$ is the minimum $k$ for which $G$ has an edge irregular total $k$-labeling. Al-Mushayt et al. 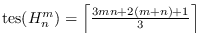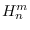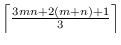“prove" that $\mathrm{tes}(H_n^m)=\left\lceil\frac{3mn+2(m+n)+1}{3}\right\rceil$ for the hexagonal grid graph $H_n^m$, but the labeling they constructed is actually not a total $\left\lceil\frac{3mn+2(m+n)+1}{3}\right\rceil$-labeling. 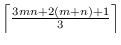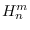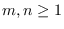In this paper, we first describe a correct edge irregular total $\left\lceil\frac{3mn+2(m+n)+1}{3}\right\rceil$-labeling of $H_n^m$ for any $m, n\geq 1$, and so show that $\mathrm{tes}(H_n^m)=\left\lceil\frac{3mn+2(m+n)+1}{3}\right\rceil$. 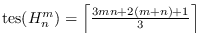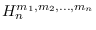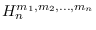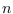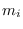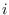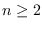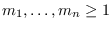Moreover, we determine the exact value of the total edge irregularity strength for a more general hexagonal grid graph $H_n^{m_1,m_2,\ldots,m_n}$ by giving an edge irregular total tes$(H_n^{m_1,m_2,\ldots,m_n})$-labeling, where $H_n^{m_1,m_2,\ldots,m_n}$ consists of $n$ columns of hexagons and has $m_i$ hexagons in the $i$-th column, $n\geq 2$, and $m_1, \ldots, m_n \geq 1$.

Key Words: Graph labelings, edge irregular total labelings, the total edge irregularity strength, hexagonal grid graphs.

2020 Mathematics Subject Classification: Primary 05C78, 52C05.

Download the paper in pdf format here.