It is known that
strongly involutive polyhedra are closely related to self-dual maps where the antipodal function acts as duality isomorphism. Such a family of polyhedra appears in different combinatorial, topological and geometric contexts, and is thus attractive to be studied. In this note, we determine the 10
antipodal pairings among the classification of the 24 self-dual pairings
Dual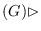 Aut
Aut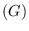
of self-dual maps
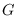
. We also present the
orbifold associated to each antipodal pairing and describe explicitly the corresponding
fundamental regions.
We finally explain how to construct two infinite families of
strongly involutive polyhedra (one of them new) by using their
doodles and the action of the corresponding orbifolds.