Ranran Wang, Fei Wen, Mengyue Yuan: Some degree sequences are determined by Laplacian spectra of the corresponding graphs, 49-70

Abstract:

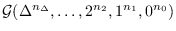
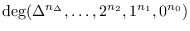
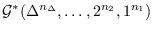
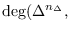
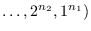
Let $\mathcal{G}(\Delta^{n_{\Delta}},\ldots, 2^{n_{2}}, 1^{n_{1}}, 0^{n_{0}})$ be the set of simple graphs with the degree sequence ${\rm deg}(\Delta^{n_{\Delta}}, \ldots, 2^{n_{2}}, 1^{n_{1}},0^{n_{0}})$, and $\mathcal{G}^{*}(\Delta^{n_{\Delta}},\ldots, 2^{n_{2}}, 1^{n_{1}})$ the set of connected graphs with the degree sequence ${\rm deg}(\Delta^{n_{\Delta}},$ $\ldots, 2^{n_{2}}, 1^{n_{1}})$. 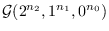In this paper, we first give the numbers of spanning tree of a bicyclic graph as well as a tricyclic graph, and then show that some degree sequences of graphs in $\mathcal{G}(2^{n_{2}}, 1^{n_{1}}, 0^{n_{0}})$ (resp. 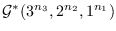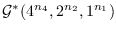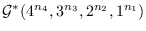$\mathcal{G}^{*}(3^{n_{3}}, 2^{n_{2}}, 1^{n_{1}})$, $\mathcal{G}^{*}(4^{n_{4}}, 2^{n_{2}}, 1^{n_{1}})$ and $\mathcal{G}^{*}(4^{n_{4}}, 3^{n_{3}}, 2^{n_{2}}, 1^{n_{1}})$) are determined by Laplacian spectra (write as DLS for short) of the corresponding graphs. 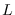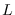Moreover, for the non-DLS degree sequences we present some $L$-cospectral mates to indicate that their $L$-cospectral degree sequences do exist. By the way, all of these extend the previous results about Laplacian spectral determinations of some degree sequences in [23]. Besides, we revise the references of Theorems 6 and 7 in [23].

Key Words: Spanning tree, Laplacian spectrum, determined by Laplacian spectrum, degree sequence, cospectral graph.

2020 Mathematics Subject Classification: 05C07, 05C50.

Download the paper in pdf format here.