Peiyi Shen, Liping Yuan, Tudor Zamfirescu: Zero forcing density of Archimedean tiling graphs, 449-462

Abstract:

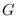
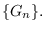
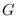
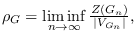
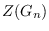
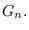
This paper mainly discusses the zero forcing density of infinite graphs. 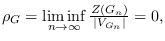When $G$ is an infinite graph, arrange all distinct finite subgraphs of G in a sequence $\{G_{n}\}.$ The zero forcing density of $G$ is defined by $\rho_{G}=\liminf\limits_{n\rightarrow\infty} \frac{Z(G_{n})}{\vert V_{G_{n}}\vert},$ where $Z(G_{n})$ is the zero forcing number of $G_{n}.$ When $\rho_{G}=\liminf\limits_{n\rightarrow\infty} \frac{Z(G_{n})}{\vert V_{G_{n}}\vert}=0,$ then we define the second density as $\rho_{G}'=\liminf\limits_{n\rightarrow\infty} \frac{Z(G_{n})}{\sqrt{\vert V_{G_{n}}\vert}}.$ 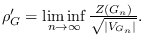Considering the eleven Archimedean tiling graphs, we get upper bounds of zero forcing density of the tilings $(3^{4},6)$ , $(3^{2},4,3,4),$ $(4,8^{2}),$ $(3,6,3,6),$ $(3,12^{2})$. 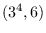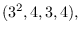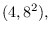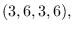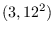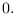The zero forcing density of the other six graphs is $0.$ Then we obtain upper bounds of the second density of these six Archimedean tiling graphs.

Key Words: Zero forcing density, zero forcing set, Archimedean tiling.

2010 Mathematics Subject Classification: Primary 05C69; Secondary 52C20.