In this note we look at the freeness for complex affine
hypersurfaces. If
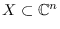
is such a hypersurface,
and
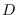
denotes the associated projective hypersurface, obtained by
taking the closure of
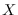
in
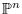
, then we relate first
the Jacobian syzygies of
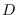
and those of
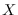
. Then we introduce two
types of freeness for an affine hypersurface
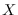
, and prove various
relations between them and the freeness of the projective
hypersurface
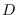
. We write down a proof of the folklore result
saying that an affine hypersurface is free if and only if all of its
singularities are free, in the sense of K. Saito's definition in the
local setting. In particular, smooth affine hypersurfaces and affine
plane curves are always free. Some other results, involving global
Tjurina numbers and minimal degrees of non trivial syzygies are also
explored.