Milica Jovalekic: Lower bound for the diameter of planar Brownian motion, 281-284

Abstract:

Let $\mathrm{B}(t)$ be a standard planar Brownian motion and $\mathrm{r}(\theta)$ be the diameter of the projection of $\mathrm{B}\left([0,1]\right)$ on the line generated by the unit vector $\mathrm{e}_\theta=(\cos\theta,\sin\theta)$, where $0\leq\theta\leq\pi$. In this short note, we find the common cumulative distribution function $F$ of the random variables $\mathrm{r}(\theta)$. Namely, we prove that

$$F(x)=8\sum_{n=1}^\infty\left(\frac{1}{x^2}+\frac{1}{(2n-1)^2\pi^2}\right)\exp\left({-\frac{(2n-1)^2\pi^2}{2x^2}}\right),$$

for every $x>0$. As immediate consequence, lower bound for the expected diameter of the set $\mathrm{B}\left([0,1]\right)$, better than known, is obtained. Namely, it is known that $\mathbb{E}\mathrm{d}\geq 1.601$, where $\mathrm{d}$ is the diameter of the set $\mathrm{B}\left([0,1]\right)$. In this note we show $\mathbb{E}\mathrm{d}\geq 1.856$.

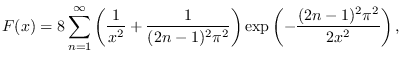
Key Words: Brownian motion, diameter, distribution, expectation.

2010 Mathematics Subject Classification: Primary 60J65; Secondary 60E05.