Themba Dube: On the socle of an algebraic frame, 371-385

Abstract:

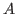
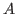
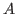
We define the socle of a frame to be the join of its complemented atoms. This turns out to be a "conservative" definition, in the sense that for any reduced ring $A$, the socle of $A$ (as classically defined to be the sum of its minimal ideals) is exactly the socle of the frame of radical ideals of $A$. We prove that the socle of an algebraic frame (not necessarily compact) is the join of compact elements whose pseudocomplements are meets of finitely many maximal elements. This substantially extends the characterization of the socle of a ring as the ideal consisting of all elements whose annihilator ideals are intersections of finitely many maximal ideals. We conclude by showing that the socle of a coproduct of two frames is the "tensor sum" of the socles of the summands.

Key Words: Algebraic frame, socle, reduced ring, radical ideal.

2010 Mathematics Subject Classification: Primary 06D22; Secondary 13A15.