Nero Budur, Pietro Gatti, Yongqiang Liu, Botong Wang: On the length of perverse sheaves and 𝒟-modules, 355-369

Abstract:

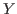
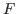
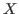
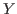
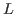
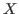
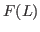
We prove that the length function for perverse sheaves and algebraic regular holonomic 𝒟-modules on a smooth complex variety $Y$ is an absolute ℚ-constructible function. One consequence is: for "any" fixed natural (derived) functor $F$ between constructible complexes or perverse sheaves on two smooth varieties $X$ and $Y$, the loci of rank one local systems $L$ on $X$ whose image $F(L)$ has prescribed length are Zariski constructible subsets defined over ℚ, obtained from finitely many torsion-translated complex affine algebraic subtori of the moduli of rank one local systems via a finite sequence of taking union, intersection, and complement.

Key Words: Length of 𝒟-modules, perverse sheaves, local systems, decomposition theorem.

2010 Mathematics Subject Classification: Primary 32S60; Secondary 14F10, 55N33, 32C38.