Let
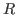
be a ring and
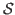
be a class of some finitely generated left
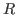
-modules. Then a left
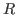
-module
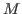
is called
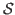
-projective if for every homomorphism
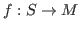
, where
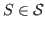
, there exist homomorphisms
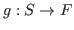
and
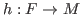
such that
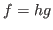
, where
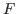
is a free module . In this paper, we give some characterizations of the following four classes of rings: (1). every injective left
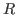
-module is
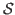
-projective; (2). every left
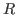
-module has a monic
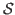
-projective preenvelope; (3). every submodule of a projective left
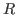
-module is
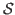
-projective; (4). every left
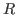
-module has an epic
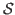
-projective envelope. Some applications are given.
-projective modules,
-
-coherent rings,
-F rings,
-semihereditary rings.