Özkan Öcalan: An improved oscillation criterion for first order difference equations, p.65-73

Abstract:

This paper is concerned with the oscillatory behavior of first order difference equation with general argument where $\left( p(n)\right)$ is a sequence of nonnegative real numbers and $% \left( \tau (n)\right)$ is a sequence of integers. Let the number $m$ be defined by $$m=\liminf_{n\rightarrow \infty }\dsum\limits_{j=\tau (n)}^{n-1}p(j)\left( \frac{j-\tau (j)+1}{j-\tau (j)}\right) ^{j-\tau (j)+1}$$. 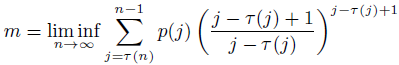It is proved that, all solutions of Equation ($\star$) oscillate if the condition m>1 is satisfied.

Key Words: Delay difference equation, general argument, oscillation.

2000 Mathematics Subject Classification: Primary: 39A10;
Secondary: 39A21.