Adrian Manea: The Ext Ring of Koszul Rings, p.51-63

Abstract:

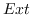
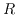
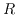
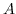
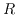
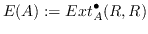
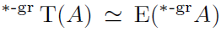
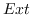
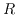
The aim of this article is to study the $\dr{Ext}$ ring associated to a Koszul $R$-ring and to use it to provide further characterisations of the latter. As such, for $R$ being a semisimple ring and $A$ a graded Koszul $R$-ring, we will prove that there is an isomorphism of DG rings between $\kal{E}(A):=\dr{Ext}^\bullet_A(R,R)$ and $\lgr\dr{T}(A) \simeq \dr{E}(\lgrr A)$. 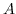Also, the $\dr{Ext}$ $R$-ring will prove to be isomorphic to the shriek ring of the left graded dual of $A$, namely $\kal{E}(A) \simeq (\lgrr A)^!$. 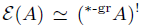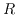As an application, these isomorphisms will be studied in the context of incidence $R$-(co)rings for Koszul posets. 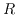Thus, we will obtain a description and method of computing the shriek ring for K $\Bbbk^c[\kal{P}]$, the incidence $R$-coring of a Koszul poset. Another application is provided for monoid rings associated to submonoids of $\bb{Z}^n$.

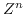
Key Words: Koszul rings, Koszul corings, Koszul pairs, $\dr{Ext}$ ring.

2000 Mathematics Subject Classification: Primary: 16E40;
Secondary: 16T15, 16E30.