G. Lusztig: Restriction of a character sheaf to conjugacy classes, p.297-309

Abstract:

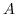
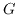
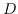
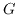
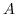
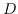
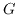
Let $A$ be a character sheaf on a connected reductive group $G$ over an algebraically closed field. Assuming that the characteristic is not bad we show that for certain conjugacy classes $D$ in $G$, the restriction of $A$ to $D$ is a local system up to shift. We also give a parametrization of unipotent cuspidal character sheaves of $G$ in terms of restriction to conjugacy classes. Without restriction on characteristic we define canonical bijections from the set of unipotent representations of the corresponding split group over a finite field to a set combinatorially defined in terms of the Weyl group.

Key Words: Reductive group, conjugacy classes, character sheaves.

2000 Mathematics Subject Classification: Primary: 20G99.

Download the paper in pdf format here.