Alexandru Buium: Transcendental numbers as solutions to arithmetic differential equations, p.245-255

Abstract:

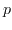
Arithmetic differential equations are analogues of algebraic differential equations in which derivative operators acting on functions are replaced by Fermat quotient operators acting on numbers. 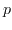Now, various remarkable transcendental functions are solutions to algebraic differential equations; in this note we show that, in a similar way, some remarkable $p$-adic transcendental numbers (including certain "$p$-adic periods") are solutions to arithmetic differential equations. Inspired by a recent paper of Manin, we then speculate on the possibility of understanding the algebraic relations among periods via Galois groups of arithmetic differential equations.

Key Words: Transcendental numbers.

2000 Mathematics Subject Classification: Primary: 11E57;
Secondary: 12H05.

Download the paper in pdf format here.