Gwénaël Massuyeau, Alexandru Oancea, Dietmar A. Salamon: Lefschetz fibrations, intersection numbers, and representations of the framed braid group, p.435-486

Abstract:

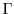
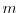
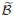
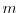
We examine the action of the fundamental group $\Gamma$ of a Riemann surface with $m$ punctures on the middle dimensional homology of a regular fiber in a Lefschetz fibration, and describe to what extent this action can be recovered from the intersection numbers of vanishing cycles. 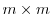Basis changes for the vanishing cycles result in a nonlinear action of the framed braid group $\tcB$ on $m$ strings on a suitable space of $m\times m$ matrices. 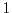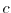This action is determined by a family of cohomologous $1$-cocycles $\cS_c:\tcB\to\GL_m(\Z[\Gamma])$ parametrized by distinguished configurations $c$ of embedded paths from the regular value to the critical values. In the case of the disc, we compare this family of cocycles with the Magnus cocycles given by Fox calculus and consider some abelian reductions giving rise to linear representations of braid groups. We also prove that, still in the case of the disc, the intersection numbers along straight lines, which conjecturally make sense in infinite dimensional situations, carry all the relevant information.

Key Words: Lefschetz fibration, braid group, mapping class group, monodromy.

2000 Mathematics Subject Classification: Primary: 14D05
16T05;
Secondary: 20F36.

Download the paper in pdf format here.