This article presents a decreasing directed paths algorithm for the parametric minimum flow problem. The algorithm always finds a shortest conditional decreasing directed path from the source node to the sink node in a parametric residual network and decreases the flow along the corresponding path in the original parametric network. On each of the iterations, the shortest conditional decreasing path (SCDP) algorithm computes a sub-interval of the parameter value within a decreasing of flow is possible and the maximum amount by which the flow can be decreased. The complexity of the SCDP algorithm is
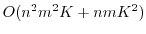
where
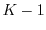
is the number of breakpoints of the piecewise linear minimum flow value function,
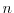
and
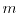
being respectively the number of nodes and the number of arcs in the network.