Mihai Epure and Alexandru Gica: Principal quadratic real fields in connection with some additive problems, p.251-259

Abstract:

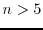
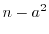
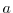
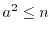
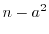
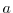
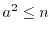
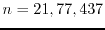
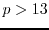
We first analyse the set of positive integers $n>5$ for which $n-a^2$ is four times a prime number for any positive odd integer $a$ such that $a^2\leq n$ and for which $n-a^2$ is a prime number for any positive even integer $a$ such that $a^2\leq n$. There are only three numbers with these properties: $n=21,77,437$. 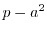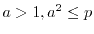The second aim is to show that there are only five prime numbers $p>13$ such that $p-a^2$ is four times a prime number for any odd positive integer $a>1,a^2\leq p$ ; namely $p=17,37,101,197,677$. 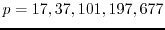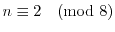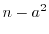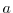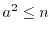The third purpose is to show that there are only four positive integers $n\equiv 2\pmod 8$ such that $n-a^2$ is the double of a prime number for any nonnegative even integer $a$ such that $a^2\leq n$; namely $n=10,26,62,362$. 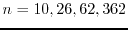The tools for proving these results belong to algebraic number theory. The key is to point out some connections between these additive problems and the class numbers for some quadratic real fields.

Key Words: Class number, sum of squares and primes, principal quadratic real fields.

2000 Mathematics Subject Classification: Primary: 11R29;
Secondary: 11P99.

Download the paper in pdf format here.