Samira Ala, Ghasem Alizadeh Afrouzi and Asadollah Niknam: Existence of positive solutions for $(p(x),q(x))$ Laplacian system, p.153-162

Abstract:

We consider the system of differential equations
$$(P)\left\{ \begin{array}{lll} -\Delta _{p(x)}u=\lambda_{1}^{p(... ...u=v=0 & \text{on }\partial \Omega , & \\ & & \end{array}\right.$$
where $\Omega \subset\mathbb{R}^{N}$ is a bounded domain with $C^{2}$ boundary $\partial \Omega ,1<p(x), q(x)\in C^{1}(\bar{\Omega})$ are functions, the operator $\Delta _{p(x)}u=div(\vert\nabla u\vert^{p(x)-2}\nabla u)$ is called $p(x)$-Laplacian $\lambda_{1},\lambda_{2}$, $\mu_{1}$ and $\mu_{2}$ are positive parameters and $g, c$ are continuous functions and $f, h, a, b$ are $C^{1}$ nondecreasing functions satisfying $f(0), h(0), a(0), b(0)\geq 0$. We discuss the existence of positive solution via sub-super solutions.

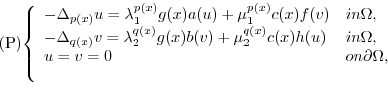
Key Words: Positive solutions; $p(x)$-Laplacian Problems; sub-supersolution.

2000 Mathematics Subject Classification: Primary: 34B15;
Secondary: 35B38, 58E05.

Download the paper in pdf format here.