We introduce three notions of inclusions of C*-algebras: with the
ideal
property, with the weak ideal property, and with topological
dimension zero. We characterize these notions and we show that for an inclusion
of C*-algebras, the ideal property
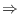
the weak ideal property
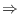
topological dimension zero. We prove that any two of these three notions do not coincide in general,
but they are all equivalent in many interesting cases. We show some permanence properties
for these notions, and we prove that they behave well with respect to tensor
products and crossed products by discrete (finite) groups, in many interesting cases.
For example, we prove that if
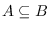
is an inclusion of C*-algebras which
has topological dimension zero and
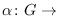
Aut
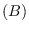
is a strongly pointwise
outer action of a finite group
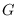
on
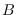
and if
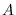
is
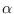
-invariant,
then the inclusion of crossed products
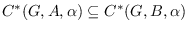
has topological dimension zero.
We show that for an inclusion of C*-algebras, the real rank zero
(in the sense of Gabe and Neagu [5])
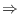
the ideal property, and
that these two notions do not coincide in general.