We provide upper bounds for the sum of the multiplicities of the
non-constant irreducible factors that appear in the canonical
decomposition of a polynomial
![$f(X)\in\mathbb{Z}[X]$](img1.png)
, in case all
the roots of
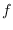
lie inside an Apollonius circle associated to two
points on the real axis with integer abscissae
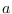
and
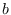
, with
ratio of the distances to these points depending on the admissible
divisors of
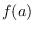
and
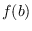
. In particular, we obtain such upper
bounds for the case where
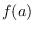
and
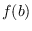
have few prime factors,
and
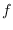
is an Eneström-Kakeya polynomial, or a Littlewood
polynomial, or has a large leading coefficient. Similar results are
also obtained for multivariate polynomials over arbitrary fields, in
a non-Archimedean setting.