Guillaume Ducoffe: A variation of Boolean distance, 405-419

Abstract:

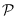
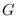
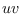
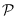
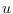
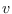
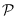
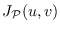
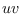
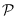
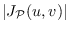
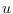
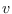
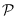
Let ${\cal P}$ be a family of paths in a connected graph $G$ so that there exists a $uv$-path in ${\cal P}$ for every choice of vertices $u$ and $v$. The ${\cal P}$-interval $J_{\cal P}(u,v)$ is the union of vertex sets of all $uv$-paths in ${\cal P}$. We address the problem of maximizing $\vert J_{\cal P}(u,v)\vert$ over all vertices $u$ and $v$, for various families ${\cal P}$ of paths.

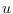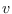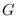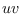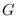• First, the Boolean distance between two vertices $u$ and $v$, in a connected graph $G$, equals the total number of vertices on $uv$-paths. The Boolean diameter of a connected graph is its maximum Boolean distance. We observe that the Boolean diameter of any graph $G$ can be computed in linear time, due to an elegant characterization of Boolean distances by [Harary, Melter, Peled & Tomescu; Discr. Math. 1982].
• Then, we restrict our study to induced paths. Unless P=NP, we cannot compute in polynomial time the maximum number of vertices on all induced paths between two vertices. However, on the positive side, we can solve this problem in polynomial time on graphs of bounded clique-width, and even in linear time on bounded-treewidth graphs and distance-hereditary graphs.
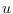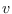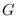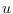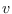• Finally, we introduce the interval semidistance for graphs, that only accounts for vertices on shortest paths. Equivalently, the interval semidistance between two vertices $u$ and $v$, in a connected graph $G$, equals the number of vertices that are metrically between $u$ and $v$. The interval diameter (maximum interval semidistance) can be computed in 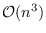${\cal O}(n^3)$ time for 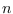$n$-vertex connected graphs. We prove that in contrast to Boolean diameter there is an 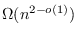$\Omega(n^{2-o(1)})$ time lower bound for this problem under the Strong Exponential-Time Hypothesis, even for graphs with only 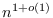$n^{1+o(1)}$ edges. However, on the positive side, we present linear-time algorithms for computing the interval diameter within various graph classes with tree-likeness properties, such as: trees, cacti, block graphs and distance-hereditary graphs.

Key Words: Boolean distance, intervals of graphs, transit functions, NP-hardness, SETH-hardness.

2010 Mathematics Subject Classification: Primary: 05C85, 05C12.

Download the paper in pdf format here.