Let
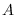
and
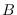
be C*-algebras such that
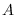
or
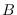
is exact.
We describe the largest ideal in
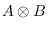
which has the
weak ideal property. For many C*-algebras
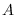
and
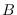
as above
we characterize when the largest ideal in
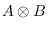
which
has the weak ideal property is the tensor product of the largest
ideals in
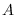
and
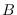
which have the weak ideal property (this is
not always true if
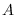
or
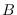
is exact). Assume that the C*-algebras
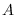
and
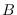
have the weak ideal property (and one of them is
exact).
We characterize (in an interesting particular case and also in
general) when
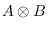
has the weak ideal property (these
two characterizations are totally different in nature).