Cornel Pasnicu: On the weak ideal property and some related properties, 147-157

Abstract:

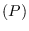
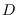
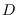
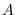
Let $(P)$ be any of the following properties: the weak ideal property, the topological dimension zero, the combination of pure infiniteness and the ideal property, residual (SP), pure infiniteness, strong pure infiniteness, provided that the zero C*-algebra is included, and $D$-stability for a separable unital strongly self-absorbing C*-algebra $D$. 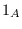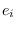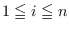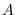Let $A$ be a separable unital C*-algebra with unit $1_{A}$, and assume that there exist non-zero projections $e_{i}$,  $1 \leqq i \leqq n$, in $A$ such that $\sum_{i=1}^{n} e_{i} = 1_{A}$. 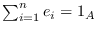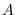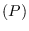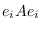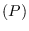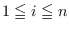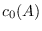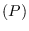We show that $A$ has $(P)$  $\Leftrightarrow$  $e_{i} A e_{i}$ has $(P)$ for every $1 \leqq i \leqq n$  $\Leftrightarrow$  $c_{0} (A)$ has $(P)$ (in fact, we prove a much more general result). 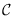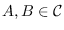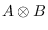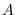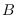We also show that, somehow surprisingly, for two large classes $\mathcal{C}$ of non-zero C*-algebras, if $A, B \in \mathcal{C}$, then the fact that $A \otimes B$ has the weak ideal property implies (or, is equivalent to) the fact that $A$ and $B$ have the weak ideal property. We prove that one of these two results still holds if we replace the weak ideal property by some related properties.

Key Words: Weak ideal property, topological dimension zero, ideal property, tensor product C*-algebra, type I C*-algebra.

2010 Mathematics Subject Classification: Primary 46L06; Secondary 46L05.