Kazem Khashyarmanesh, Mehrdad Nasernejad, Jonathan Toledo: Symbolic strong persistence property under monomial operations and strong persistence property of cover ideals, 105-131

Abstract:

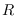
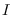
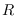
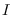
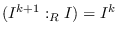
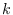
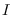
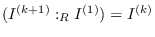
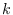
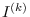
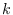
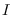
Let $R$ be a commutative Noetherian ring and $I$ be an ideal of $R$. Then, $I$ has the strong persistence property if $(I^{k+1}:_R I)=I^k$ for all $k$. Also, we say that $I$ has the symbolic strong persistence property if $(I^{(k+1)}:_R I^{(1)})=I^{(k)}$ for all $k$, where $I^{(k)}$ denotes the $k$-th symbolic power of $I$. In this paper, by using some monomial operations, such as expansion, weighting, monomial multiple, monomial localization, and contraction, we introduce several methods for constructing new monomial ideals which have the symbolic strong persistence property based on the monomial ideals which have the symbolic strong persistence property. We also probe the strong persistence property of the cover ideal of the union of two finite simple graphs.

Key Words: Strong persistence property, associated primes, cover ideals, symbolic strong persistence property.

2010 Mathematics Subject Classification: Primary 13C13, 13B25, 13A30, 05E40; Secondary 13P25, 05C25.