Sizhong Zhou: A result on restricted fractional $(g,f)$-factors in graphs, 407-416

Abstract:

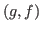
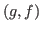
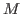
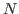
In the NFV network, the availability of resource scheduling can be transformed to the existence of the restricted fractional $(g,f)$-factors in the corresponding NFV network graph. Researching on the existence of the restricted fractional $(g,f)$-factors in network structure can help to construct the NFV network with the efficient application of resources. 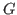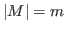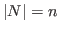Let $M$ and $N$ be two sets of independent edges of $G$ with $\vert M\vert=m$, $\vert N\vert=n$ and $M\cap N=\emptyset$. 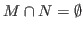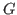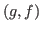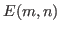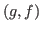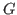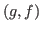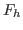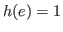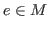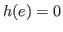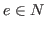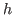We say that $G$ contains a fractional $(g,f)$-factor with the property $E(m,n)$ (or a restricted fractional $(g,f)$-factor) if $G$ has a fractional $(g,f)$-factor $F_h$ such that $h(e)=1$ for any $e\in M$ and $h(e)=0$ for any $e\in N$, where $h$ is its indicator function with $h(e)\in[0,1]$ for any $e\in E(G)$. 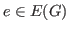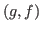In this paper, a sufficient condition for graphs to possess restricted fractional $(g,f)$-factors is presented. Furthermore, it is shown that this result is best possible in some sense.

Key Words: Network, graph, neighborhood of independent set, minimum degree, restricted fractional $(g,f)$-factor.

2020 Mathematics Subject Classification: Primary 05C70; Secondary 68M10.