Prasanna Kumar, Ritu Dhankha: Some refinements of inequalities for polynomials, 359-367

Abstract:

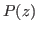
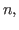
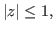
If $P(z)$ is a polynomial of degree $n,$ having all its zeros in $\vert z\vert\leq 1,$ then Turán [18] proved that

$$\max_{\vert z\vert=1}{\vert P'(z)\vert}\geq \frac{n}{2}\max_{\vert z\vert=1}{\vert P(z)\vert}.$$

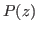
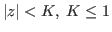
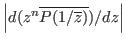
We prove a generalization of the above inequality to the class of polynomials having all their zeros in $\vert z\vert\leq K,K\geq 1.$ We also prove an inequality for the derivative of a polynomial $P(z)$ having no zeros in the disc $\vert z\vert<K,\;K\leq 1$ whenever $\vert P'(z)\vert,$ and $\left\vert d(z^n\overline{P(1/\overline{z})})/dz\right\vert$ attain maximum at a same point on $\vert z\vert=1.$ 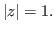Both the results generalize and sharpen several of the known results in this direction. We also present two examples to show that in some cases the bounds obtained by our results can be considerably sharper than the known bounds. Further, these results have been extended to polar derivatives of polynomials also.

Key Words: Inequalities, polynomials, zeros.
2010 Mathematics Subject Classification: Primary 30A10; Secondary 30D15.