Vinay Kumar Jain: Generalizations of certain ineqalities for $s^{th}$ derivative of a polynomia, 261-270

Abstract:

For an arbitrary polynomial $f(z)$, let

$$\nonumber \Vert f\Vert _q = \left\{ \frac{1}{2\pi} \int_{0... ...i}\vert f(e^{i\theta})\vert^q d\theta \right\}^{1/q} , q > 0.$$

It is known for a polynomial $p(z) = \sum_{j=0}^{n} a_jz^j$ of degree $n$, having no zeros in
$\vert z\vert < k, (k \geq 1)$ that

$$\nonumber \Vert p^{(s)}\Vert _q \leq \frac{n(n-1)\hdots (n... ...vert+\vert a_s\vert k^{s+1}} \right\},\textrm{ } 1 \leq s < n$$

and

$$\nonumber \max_{\vert z\vert=1}\vert p^{(s)}(z)\vert \leq ... ...vert p(z)\vert -\min_{\vert z\vert=k}\vert p(z)\vert\right\}.$$

By considering polynomial $p(z)$ of degree $n$, in the form $a_0 + \sum_{j=t}^{n}a_jz^j, (1 \leq t \leq n$), having no zeros in $\vert z\vert < k, (k \geq 1)$, with

$$\gamma_s(\vert a_0\vert)= \gamma_s = \left\{\begin{array}... ...s \geq t, \end{array} \right.\hspace{.5in} ,1 \leq s \leq n,$$

we have obtained the generalization of the known result in the form

$$\nonumber \Vert p^{(s)}\Vert _q \leq \frac{n(n-1)\hdots (n-s+1)}{\Vert\gamma_s + z\Vert _q} \Vert p\Vert _q$$

and

$$\nonumber \max_{\vert z\vert=1}\vert p^{(s)}(z)\vert \leq ... ...\right\},\textrm{ } m = \min_{\vert z\vert=k}\vert p(z)\vert.$$

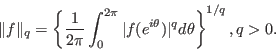Key Words: The $s^{th}$ derivative of polynomial, generalizations,

no zeros in $\vert z\vert < k, (k \geq 1)$, inequalities.

2010 Mathematics Subject Classification: Primary 30C10; Secondary 30A10.