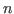Let
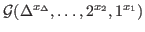
be the set of connected graph with degree sequence
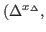
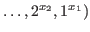
. In this paper,
we show that the degree sequences of
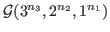
and
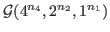
are determined by Laplacian
spectrum with some restrictions. By those results we obtain that
sun graph [4],
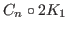
[6]
and
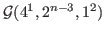
are determined by their Laplacian
spectra. Furthermore, we prove that any graph
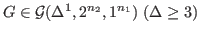
, whose
degree sequence is determined by Laplacian spectrum except that
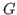
is a bicyclic graph with
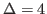
. Moreover, if
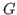
is a bicyclic graph with
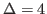
, then
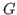
may be
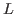
-cospectral to a graph with degree
sequence
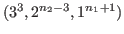
. Applying this result
we conclude that some graphs such as
starlike
trees[22],
unicyclic graph 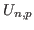
[27],
friendship graph and
butterfly graph et al. are
determined by their Laplacian spectra. Moreover, we give a
Laplacian spectral characterization of the degree sequence of
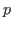
-rose graph which supports Liu's conjecture [19].with