Zhiren Sun, Sizhong Zhou: Notes on fractional $(a,b,k)$-critical covered graphs, 105-115

Abstract:

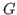
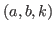
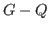
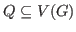
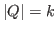
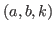
A graph $G$ is called fractional $(a,b,k)$-critical covered if $G-Q$ is fractional $[a,b]$-covered for any $Q\subseteq V(G)$ with $\vert Q\vert=k$. In this article, we demonstrate an independence number and minimum degree condition for a graph to be fractional $(a,b,k)$-critical covered, which is a generalization of Zhou's previous result [S. 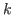Zhou, Some new sufficient conditions for graphs to have fractional $k$-factors, International Journal of Computer Mathematics 88(3)(2011)484-490]. Furthermore, we demonstrate that two conditions on independence number and minimum degree in our main result are sharp.

Key Words: Graph, independence number, minimum degree, fractional $[a,b]$-covered graph, fractional $(a,b,k)$-critical covered graph.

2010 Mathematics Subject Classification: Primary 05C70; Secondary 68M10.