Abstract:
We introduce the notion of general prints of a word, which is substantialized by certain canonical decompositions, to study repetition in words. These associated decompositions, when applied recursively on a word, result in what we term as core prints of the word. The length of the path to attain a core print of a general word is scrutinized. This paper also studies the class of square-free ternary words with respect to the Parikh matrix mapping, which is an extension of the classical Parikh mapping. It is shown that there are only finitely many matrix-equivalence classes of ternary words such that all words in each class are square-free. Finally, we employ square-free morphisms to generate infinitely many pairs of square-free ternary words that share the same Parikh matrix.
Key Words: General print, core print, square-free, 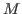 -equivalence.
-equivalence.
2010 Mathematics Subject Classification: Primary 68R15, 68Q45, 05A05.
-equivalence.