Takafumi Miyazaki: Application of cubic residue theory to an exponential equation concerning Eisenstein triples, 305-312

Abstract:

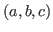
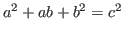
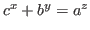
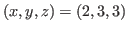
For any triple $(a,b,c)$ of pair-wise coprime positive integers satisfying $a^2+ab+b^2=c^2$, we study the exponential Diophantine equation $c^x+b^y=a^z$. First, we conjecture that the equation has no positive solution other than $(x,y,z)=(2,3,3)$. Second, we prove that our conjecture is true under certain congruence conditions on a, b and c. The proof relies upon the theory of cubic residue and several existing results concerning the generalized Fermat equation $X^3+Y^{3}=Z^n$. 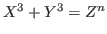Our result can be regarded as a relevant analogue to some results on Jesmanowicz' conjecture concerning Pythagorean triples.

Key Words: Exponential Diophantine equation, cubic residue, generalized Fermat equation.

2010 Mathematics Subject Classification: Primary 11D61; Secondary 11A15; 11D41.