From Mersenne sequence to elliptic divisibility sequence, it is a important problem in number theory to prove the existence of primitive prime divisors of an arithmetically defined sequence, i.e., the finiteness of the relevant Zsigmondy set. In this paper, we prove that the Zsigmondy set defined by iteration of weighted homogeneous polynomial is a finite set. In other words, let
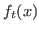
be a weighted homogeneous polynomial of degree

and weight

Let
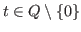
and let

be the Zsigmondy set for the zero orbit

then there exists a constant
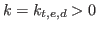
such that
