Samir Aberkane, Vasile Dragan, Ioan-Lucian Popa: Optimal filtering of a signal generated by a system modeled by Itô differential equations with periodic coefficients: the dichotomic case, 347-360

Abstract:

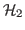
This note addresses the problem of optimal $\mathcal{H}_{2}$ filtering for a class of continuous-time time-varying stochastic systems. The time-variation character is considered to be periodic. The proposed filtering results are proved without requiring the restrictive assumption of exponential stability in the mean square of the underlying stochastic systems. Instead, we would rather assume that the Lyapunov operator associated to the dynamical stochastic system is exponentially dichotomic. The state space representation of the optimal filter is designed based on the unique periodic solution of a suitably defined Lyapunov differential equation and the periodic and stabilizing solution of a suitably defined generalized periodic Riccati differential equation.

Key Words: filtering, stochastic systems, exponential dichotomy.

2010 Mathematics Subject Classification: Primary 93E11, Secondary 34D09.