Vladimir Rasvan: Stable and critical cases in Huygens synchronization, 463-473

Abstract:

A system of equations describing two van der Pol oscillators coupled to a one-dimensional distributed environment (lossless transmission line for electronic oscillators or elastic rod for mechanical oscillators) is considered. The resulting boundary value problem with derivative boundary conditions for hyperbolic partial differential equations has its solutions in a one-to-one correspondence with the solutions of a system of functional differential equations of neutral type. 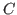The location of the eigenvalues of some matrix accounting for the so called difference operator of the system of functional differential equations introduces two cases of stability analysis: the stable case (when the aforementioned eigenvalues are located inside the unit disk of $\mathbb{C}$) and the critical case (when they are located on the unit circle). For the stable case a result of stability by the first approximation is obtained, accounting for oscillation quenching ("synchronization to zero"). The critical case remains the "big unknown" of the theory of neutral functional differential equations.

Key Words: synchronization, neutral functional differential equations, stability, strongly stable case, critical case.

2010 Mathematics Subject Classification: Primary 34D06, Secondary 34C15, 34K20, 34K40, 35B35.