Next: Seyed Shahab Arkian, Amir Mafi Up: TOME 61 (109), no. 3, 2018 Previous: Luca Amata, Marilena Crupi
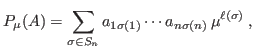
Key Words:-permanent,
-permanent, determinant, permanent, graph, tree, path, graph labeling, integer sequence, Mathematica
2010 Mathematics Subject Classification: Primary 15A15. Secondary 05C50, 05C78, 05C30, 68R10, 11B83