Shamsa Kanwal, Gerhard Pfister: Standard Bases with Special Generators of the Leading Idea, 69-81

Abstract:

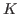
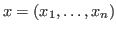
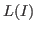
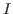
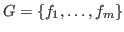
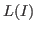
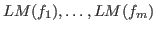
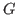
Let $I\subseteq K[x]$ be an ideal, $K$ a field, $x=(x_1,\ldots, x_n)$ and $>$ a monomial ordering (not necessarily a well-ordering). Let $L(I)$ be the leading ideal of $I$ with respect to $>$. A standard basis (in case of a well-ordering a Gröbner basis) $G=\{f_1,\ldots ,f_m\}$ is defined by the property that $L(I)$ is generated by the leading monomials $LM(f_1), \ldots, LM(f_m)$ of $G$. 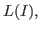Usually one considers a standard basis associated to the uniquely determined minimal system of monomials generating $L(I),$ a minimal standard basis. 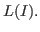In case of border bases, Janet bases or Pommaret bases (usually only defined for well-orderings but we generalize the concept to any ordering) the underlying standard bases have as leading monomials special (non minimal) generators of $L(I).$ We describe an algorithm which computes these bases using a minimal standard bases and the corresponding special generators of $L(I)$. 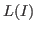We have implemented these algorithms in SINGULAR (cf. [DGPS16]) including modular and parallel implementations and give timings to compare them (cf.[KP17]). We also discuss the verification of the modular algorithm to compute border bases and Janet bases.

Key Words: Gröbner basis, standard basis, Janet Basis, Border Basis, modular computation

2010 Mathematics Subject Classification: Primary 13P99, 13E05