Mehdi Delkhosh, Kourosh Parand, Hossein Yousefi: Accurate numerical solution for a type of astrophysics equations using three classes of Euler functions, 39-49

Abstract:

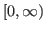
This paper presents an efficient numerical algorithm based on rational non-orthogonal basis functions derived from Euler polynomials for solving the Lane-Emden type equations as singular initial value problems on the semi-infinite interval $[0, \infty)$. These equations have been used to model several phenomena in theoretical physics, mathematical physics and astrophysics, such as the theory of stellar structure and radiative cooling. The proposed method is based on converting an ordinary nonlinear differential equation into a sequence of linear differential equations through the quasilinearization method and then are solved using the collocation method. This method reduces the solution of these problems to the solution of a system of algebraic equations to simplify the computations. The purpose of this study is solving the Lane-Emden type equations using three classes of Euler functions and providing an accurate comparison of these basis functions. Furthermore, the rational fractional Euler functions (RFE) have been introduced for the first time. Numerical results show that the performance of the three proposed basis functions is nearly equal and the method is reliable, efficient and accuracy more than numerical and analytical methods.

Key Words: Lane-Emden type equations, Nonlinear ODE, Collocation method, Quasilinearization method, Rational fractional Euler functions.

2010 Mathematics Subject Classification: Primary 34G20
Secondary 26A33, 65M70