Victor Alexandru, Marian Vâjâitu, Alexandru Zaharescu: On some modules associated with Galois orbits, 3-11

Abstract:

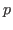
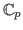
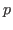
Given a prime number $p$ we consider $\mathbb{C}_p$, which is usually called the Tate field, the topological completion of the algebraic closure of the field of $p$-adic numbers. We introduce and study a class of modules associated with factor groups of profinite groups, especially of those which are the Galois groups of the normal closure of algebraic infinite extensions. 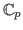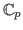In particular, we show that the module associated with a Galois orbit of an arbitrary element of $\mathbb{C}_p$ is a factor of the Iwasawa algebra of a normal element of $\mathbb{C}_p$ by an ideal which can be described.

Key words and phrases: Galois orbits, Iwasawa algebra, local fields, distributions.

2010 Mathematics Subject Classification: 11S99.