Let
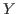
be a hypersurface in projective space having only ordinary double points as singularities. We prove a variant of a conjecture of L. Wotzlaw on an algebraic description of the graded quotients of the Hodge filtration on the top cohomology of the complement of Y except for certain degrees of the graded quotients, as well as its extension to the Milnor cohomology of a defining polynomial of Y for degrees a little bit lower than the middle. These partially generalize theorems of Griffiths and Steenbrink in the Y smooth case, and enable us to determine the structure of the pole order spectral sequence. We then get quite simple formulas for the Steenbrink and pole order spectra in this case, which cannot be extended even to the simple singularity case easily.