We solve two open problems in Finsler geometry which have been proposed by Z. Shen about
Finsler metrics with relatively isotropic Landsberg curvature and weakly Landsberg metrics. We define a new quantity which
is closely related to the S-curvature. Then, we find some conditions for
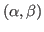
-metrics
under which the notions of relatively isotropic Landsberg curvature and relatively isotropic
mean Landsberg curvature are equivalent. It extends Cheng-Shen's well-known theorem
that proves the equality for the Randers metrics. As an application, we prove that every weakly
Landsberg
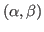
-metric of non-Randers type with vanishing S-curvature is Berwaldian.
-metric