Bradut Apostol: Asymptotic properties of some functions related to regular integers modulo n, 221-231

Abstract:

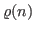
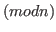
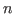
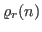
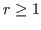
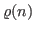
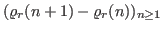
Let $\varrho(n)$ denote the number of positive regular integers $(\text{mod }n)$ less than or equal to $n$ and let $\varrho_r(n)$ ($r\geq 1$) be the multidimensional generalization of the arithmetic function $\varrho(n)$. We study the behaviour of the sequence $(\varrho_r(n+1)-\varrho_r(n))_{n\geq 1}$. 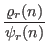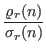We also investigate the average orders of the functions $$\frac{\varrho_r(n)}{\psi_r(n)}$$, $$\frac{\varrho_r(n)}{\sigma_r(n)}$$ and $$\frac{\varrho_r(n)}{\sigma^*_r(n)}$$. 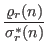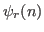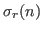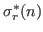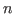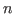Here the functions $\psi_r(n)$, $\sigma_r(n)$, $\sigma^*_r(n)$ generalize the Dedekind function, the sum of the divisors of $n$ and the sum of the unitary divisors of $n$, respectively. 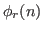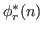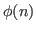Finally, we give the extremal orders of some compositions involving the functions mentioned previously and the functions $\phi_r(n)$ and $\phi_r^*(n)$ which generalize $\phi(n)$, the Euler function and the unitary function corresponding to $\phi(n)$.

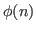
Key Words: arithmetical function, composition, regular integers $(\text{mod }n)$, average orders, extremal orders.

2010 Mathematics Subject Classification: Primary 11A25,
Secondary 11N37