In this paper, we apply several forms of generalized maximum principles to study the
uniqueness of complete spacelike hypersurfaces immersed in Lorentzian warped products.
First, we consider the cases of ambient space with vanish
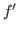
, then obtain some uniqueness
results of constant
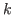
-th mean curvature. Afterwards, we obtain the sign relationship
between the support function with the derivative of warping function. By using this result,
under some suitable restriction on the higher order mean curvature, we establish the
uniqueness results of Lorentzian warped product
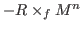
with non-vanish
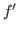
.
Furthermore, applications to such spaces are given.